
总结: 昨天晚上被蚊子咬到睡不着觉,好不容易进入梦乡,恍惚间又听到噗通一声,我当时就料想到是手机掉到床柜后面去了,于是早上七点多钟又爬起来翻箱倒柜找手机关闹钟。
所以意料当中地今天上午下午摸鱼只做了三条题目,都是比较ez的,晚上划水搭建了下博客。
701. Insert into a Binary Search Tree
Given the root node of a binary search tree (BST) and a value to be inserted into the tree, insert the value into the BST. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.
Note that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.
For example,
Given the tree:
4
/ \
2 7
/ \
1 3
And the value to insert: 5
You can return this binary search tree:
4
/ \
2 7
/ \ /
1 3 5
This tree is also valid:
5
/ \
2 7
/ \
1 3
\
4
解答:
方案1 递归解决1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) return new TreeNode(val);
if(val > root->val){
if(root->right==nullptr) root->right=new TreeNode(val);
else insertIntoBST(root->right,val);
}
else if(val < root->val){
if(root->left==nullptr) root->left=new TreeNode(val);
else insertIntoBST(root->left,val);
}
return root;
}
};
方案2 迭代求解,用时明显短于递归1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17class Solution {
public:
TreeNode* insertIntoBST(TreeNode* root, int val) {
if(!root) return new TreeNode(val);
TreeNode *p=root;
while(1){
if(val<p->val&&p->left)
p=p->left;
else if(val>p->val&&p->right)
p=p->right;
else break;
}
if(p->val <val) p->right=new TreeNode(val);
else p->left=new TreeNode(val);
return root;
}
};
原题中特地强调,可以改变树的结构,但是相对来说比较复杂,翻了翻评论区并没有这么写的解答,我思考了下,感觉与平衡二叉树的删除类似,在找到其应该插入位置后根据是否存在左右子树分类谈论。二叉树实在是太复杂啦!
235. Lowest Common Ancestor of a Binary Search Tree
- 二叉搜索树的最近公共祖先
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
According to the definition of LCA on Wikipedia: “The lowest common ancestor is defined between two nodes p and q as the lowest node in T that has both p and q as descendants (where we allow a node to be a descendant of itself).”
Given binary search tree: root = [6,2,8,0,4,7,9,null,null,3,5]
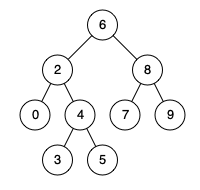
Example 1:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
Output: 6
Explanation: The LCA of nodes 2 and 8 is 6.
Example 2:
Input: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
Output: 2
Explanation: The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
Note:
All of the nodes’ values will be unique.
p and q are different and both values will exist in the BST.
解法: 递归实在是太好写啦,主要注意其二叉搜索树的特性。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if(!root) return nullptr;
if(p->val<root->val && q->val>root->val) return root;
if(p->val>root->val && q->val<root->val) return root;
if(p==root||q==root) return root;
if(p->val<root->val && q->val<root->val) return lowestCommonAncestor(root->left,p,q);
if(p->val>root->val && q->val>root->val) return lowestCommonAncestor(root->right,p,q);
return root;
}
};
589. N-ary Tree Preorder Traversal
- N叉树的前序遍历
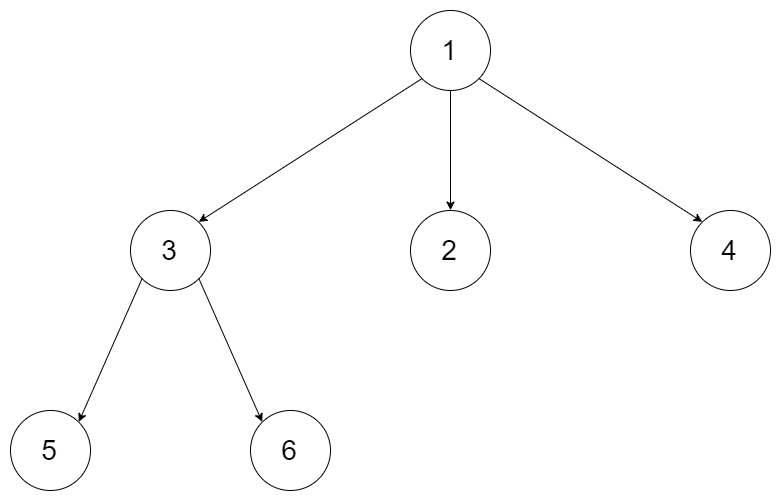
一开始写了个递归版本,发现速度很慢,想写迭代版本,但是感觉和二叉树又不太一样 参考了下评论区大神的思路 豁然开朗 随便写写写下来,
发现时间还是特别高! 非常生气地拿了80ms的源码来跑,结果虽然比我的好,还是很高。 就有点懵逼了。
感觉这个迭代写法还是可以学习一下,和之前常写的二叉树的前序遍历迭代版本不太相同。(对栈的使用)1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
// class Solution {
// public:
// vector<int> preorder(Node* root) {
// vector<int> res;
// help(root,res);
// return res;
// }
// void help(Node* p,vector<int>& res){
// if(!p) return;
// res.push_back(p->val);
// for(auto it:p->children)
// help(it,res);
// }
// };
// class Solution {
// public:
// vector<int> preorder(Node* root) {
// stack<Node*> stk;
// vector<int> res;
// if(!root) return res;
// Node* p=root;
// stk.push(p);
// while(!stk.empty()){
// p=stk.top();stk.pop();
// res.push_back(p->val);
// if(p->children.empty())
// continue;
// else{
// for(auto it=p->children.rbegin();it!=p->children.rend();it++)
// stk.push(*it);
// }
// }
// return res;
// }
// };
class Solution {
public:
vector<int> preorder(Node* root) {
vector<int> res;
if(root == nullptr) return res;
stack<Node*> st;
st.push(root);
while(!st.empty())
{
Node* t = st.top();
st.pop();
res.push_back(t->val);
for(auto r = t->children.rbegin(); r != t->children.rend(); r++)
{
st.push(*r);
}
}
return res;
}
};


