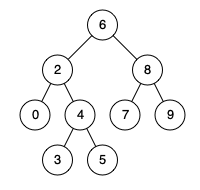
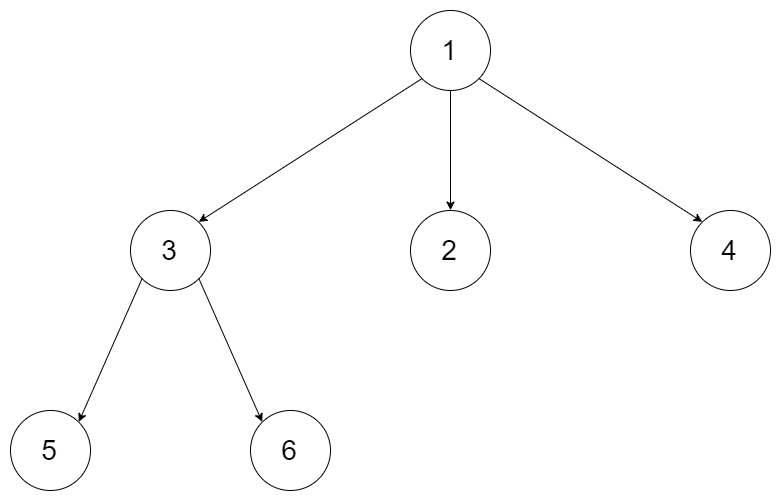
590. N-ary Tree Postorder Traversal
N叉树的后序遍历
解法一:递归1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29/*
// Definition for a Node.
class Node {
public:
int val;
vector<Node*> children;
Node() {}
Node(int _val, vector<Node*> _children) {
val = _val;
children = _children;
}
};
*/
class Solution {
public:
vector<int> postorder(Node* root) {
vector<int> res;
help(root,res);
return res;
}
void help(Node* p,vector<int>& res){
if(!p) return ;
for(auto i:p->children)
help(i,res);
res.push_back(p->val);
}
};
解法二:迭代我们也可以使用迭代的方法来做,这里有个小trick,写法跟先序遍历十分的像,不同的就是每次把从stack中取的结点的值都加到结果res的最前面,还有就是遍历子结点数组的顺序是正常的顺序,而前序遍历是从子结点数组的后面往前面遍历,这点区别一定要注意。
1 | class Solution { |
429. N-ary Tree Level Order Traversal
层次遍历,没啥好说的。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> res;
if(!root) return res;
deque<Node*> temp;
temp.push_back(root);
while(!temp.empty()){
int size=temp.size();
vector<int> t;
for(int i=0;i<size;i++){
auto it=temp.front();
temp.pop_front();
t.push_back(it->val);
for(auto j:it->children)
temp.push_back(j);
}
res.push_back(t);
t.clear();
}
return res;
}
};
559. Maximum Depth of N-ary Tree
- N叉树的最大深度
递归非常简单。。没啥好说的1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16class Solution {
public:
int maxDepth(Node* root) {
int res=0;
help(root,0,res);
return res;
}
void help(Node* p,int s,int& res) {
if(!p) return;
s++;
res=s>res? s:res;
for(auto it:p->children)
help(it,s,res);
}
};
208. Implement Trie (Prefix Tree)
比较简单的medium题了,就是比较繁琐。在定义前缀树的时候要先去检查是否已经存在该结点。感觉还是对map的使用不够熟练。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56class Node {
public:
bool isWord=false;
unordered_map<char,Node*> next;
Node() {
isWord=false;
}
Node(unordered_map<char,Node*> _next){
next=_next;
isWord=false;
}
};
class Trie {
public:
Node* root;
/** Initialize your data structure here. */
Trie() {
root=new Node();
}
/** Inserts a word into the trie. */
void insert(string word) {
Node* temp=root;
for(int i=0;i<word.length();i++){
auto it=temp->next.find(word[i]);
if(it==temp->next.end()){
temp->next[word[i]]=new Node();
temp=temp->next[word[i]];
}else temp=temp->next[word[i]];
}
temp->isWord=true;
}
/** Returns if the word is in the trie. */
bool search(string word) {
Node* temp=root;
for(int i=0;i<word.length();i++){
auto it=temp->next.count(word[i]);
if(!it) return false;
temp=temp->next[word[i]];
}
if(temp->isWord) return true;
return false;
}
/** Returns if there is any word in the trie that starts with the given prefix. */
bool startsWith(string prefix) {
Node* temp=root;
for(int i=0;i<prefix.length();i++){
if(temp->next.count(prefix[i])==0) return false;
temp=temp->next[prefix[i]];
}
return true;
}
};
677. Map Sum Pairs
- 键值映射
和上题类似,区别在于用递归思想求前缀总和。 考虑过在每个结点都写入当前值的方法,但是感觉这样每次插入新结点都需要去更新整个树,复杂度欠缺考虑。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47class Node{
public:
int num=0;
unordered_map<char,Node*> next;
Node() {}
Node(unordered_map<char,Node*> _next){
next=_next;
}
};
class MapSum {
public:
Node *root;
/** Initialize your data structure here. */
MapSum() {
root=new Node();
}
void insert(string key, int val) {
Node *temp=root;
for(int i=0;i<key.length();i++){
auto it=temp->next.find(key[i]);
if(it==temp->next.end()){
temp->next[key[i]]=new Node();
temp=temp->next[key[i]];
}
else temp=temp->next[key[i]];
}
temp->num=val;
}
int sum(string prefix) {
Node *temp=root;
for(int i=0;i<prefix.length();i++){
auto it=temp->next.find(prefix[i]);
if(it==temp->next.end()) return 0;
else temp=temp->next[prefix[i]];
}
return help(temp);
}
int help(Node *p){
int sum=p->num;
for(auto it=p->next.begin();it!=p->next.end();it++)
sum+=help(it->second);
return sum;
}
};
648. Replace Words
- 单词替换
写得有些自闭,不想说话。逻辑不难,主要是对于C++中string类的运用暂时还有所欠缺,特别对于一个长句子的处理。
1 | class Node { |